What is statistical significance?

The amount of data created in 2020 alone is estimated to be around 50.5 zettabytes (that’s 21 zeroes); some claim that data is the 21st century’s most valuable commodity—the new oil of the digital economy.

With the amount of data generated continuing to grow exponentially, analysis has become even more important. But no analysis is useful if it isn’t accurate.

What is Statistical Significance?

Statistical significance is the likelihood that a relationship between two or more variables in an analysis is not purely coincidental, but is actually caused by another factor. In other words, statistical significance is a way of mathematically proving that a certain statistic is reliable.

Why is statistical significance important to businesses?

In the real world, businesses use statistical significance to understand how strongly the results of their surveys, experiments, polls, or user data should influence their decisions.

Statistical significance is important because it gives you confidence in your analysis and its resulting insights. There is no business value in taking actions on insights that are misleading or incorrect, and what’s more, taking action on misleading information can also keep you from investing resources correctly.

How do I calculate statistical significance?

Statistical significance is often calculated with statistical hypothesis testing, which tests the validity of a hypothesis by figuring out the probability that your results have happened by chance.

Here, a “hypothesis” is an assumption or belief about the relationship between your datasets. The result of a hypothesis test allows us to see whether this assumption holds under scrutiny or not.

A standard hypothesis test relies on two hypotheses.

• Null hypothesis: The default assumption of a statistical test that you’re attempting to disprove (e.g., an increase in cost won’t affect the number of purchases).
• Alternative hypothesis: An alternate theory that contradicts your null hypothesis (e.g., an increase in cost will reduce the number of purchases). This is the hypothesis you hope to prove.

The testing part of hypothesis tests allows us to determine which theory, the null or alternative, is better supported by data. There are many hypothesis testing methodologies, and one of the most common ones is the Z-test, which is what we’ll discuss here.

But, before we get to the Z-test, it is important for us to visit some other statistical concepts the Z-test relies on.

Normal distribution

Normal distribution is used to represent how data is distributed and is primarily defined by:

• The mean (μ): The mean represents the location of the center of your data (or the average).
• The standard deviation (σ): The standard deviation is a measure of the amount of variation or dispersion of a set of values and represents the spread in your data.

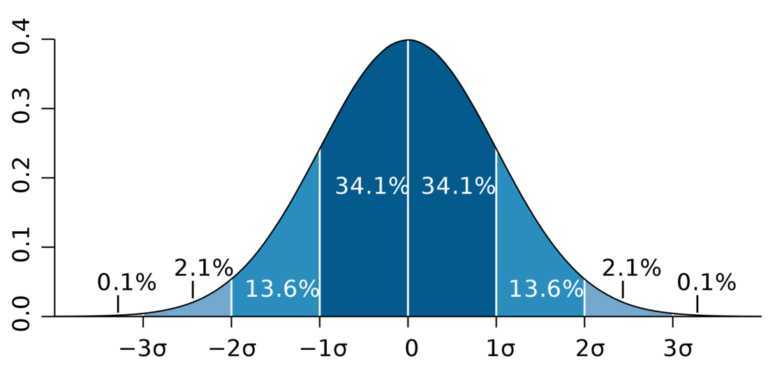
A normal distribution curve (Image source – Wikipedia)

Normal distribution is graphically depicted by what is called a “bell curve” (due to its shape). A normal distribution curve is used to assess the location of a data point in terms of the standard deviation and mean. This allows you to determine how anomalous a data point is based on how many standard deviations it is from the statistical mean. The properties of a normal distribution mean that:

• ≈68.3% of all data points are within a range of 1 standard deviation on each side of the mean.
• ≈95.4% of all data points are within a range of 2 standard deviations on each side of the mean.
• ≈99.7% of all data points are within a range of 3 standard deviations on each side of the mean.

If we have a normal distribution for a data set, we can locate any data point by the number of standard deviations it is away from the mean.

For example, let’s consider that the average number of downloads of a music streaming app is 1000, with a standard deviation of 100 downloads. If an app called MixTunes has 1200 downloads, we can say that it is 2 standard deviations above the mean and is in the top 2.3% of music apps.

Z-score

In statistics, the distance between a data point and the mean of the data set is assessed as a Z-score. The Z-score (also known as the standard score) is the number of standard deviations by which a data point is distanced from the mean. 

A Z-score is calculated by subtracting the mean of the distribution (μ) from the value of the considered data point (x) and dividing the result by the standard deviation (σ).

Z = (x – μ)/(σ)

In the example we discussed above, MixTunes would have a Z-score of 2 since the mean is 1000 downloads and the standard deviation is 100 downloads.

Assuming a normal distribution lets us determine how meaningful the result you observe in an analysis is, the higher the magnitude of the Z-score (either positive or negative), the more unlikely the result is to happen by chance, and the more likely it is to be meaningful. To quantify just how meaningful the result of your analysis is, we use one more concept.

In studies where a sample of an overall population is considered (like surveys and polls), the Z-value formula is slightly changed to account for the fact that each sample can vary from the overall population, and thus have a standard deviation from the overall distribution of all samples.

Z = (x – μ) / (σ / √n)

Here, √n is the square root of the sample size.

P-values

The final concept we need to use the Z-test is that of P-values. A P-value is the probability of finding results at least as extreme as those measured when the null hypothesis is true.

For example, say we’re measuring the average height of individuals in the US states of California and New York. We can start off with a null hypothesis that the average height of individuals in California is not higher than the average height of individuals in New York.

We then perform a study and find the average height of Californians to be higher by 1.4 inches, with a P-value of 0.48. This implies that in a world where the null hypothesis—the average height of Californians is not higher than the average height of New Yorkers—is true, there’s a 48% chance we would measure heights at least 1.4 inches higher in California.

So, if heights in California are not actually higher, we’d still measure them as higher by at least 1.4 inches about half the time due to random noise in the data. Subsequently, the lower the P-value, the more meaningful the result because it is less likely to be caused by noise or random chance.

Whether or not the result of a study or analysis can be called statistically significant depends on the “significance level” of that test study, which is established before the study begins. The significance value, denoted by the greek letter alpha (α), is nothing but the maximum P-value we can accept to consider the study statistically significant. In other words, it’s the probability of rejecting the null hypothesis when it’s true–or, simply put, the probability of making a wrong decision.

This significance value varies by situation and field of study, but the most commonly used value is 0.05, corresponding to a 5% chance of the results occurring randomly.

A Z-score can be converted to a P-value (and vice versa) using a programming language like R, or by simpler methods like an Excel formula, an online tool, a graphing calculator, or even a simple number table called the Z-score table.

Z-testing  

For a Z-test, the normal distribution curve is used as an approximation for the distribution of the test statistic. To carry out a Z-test, find a Z-score for your test or study and convert it to a P-value. If your P-value is lower than the significance level, you  can conclude that your observation is statistically significant.

Let’s take a look at an example. 

Imagine we work in the admissions department at University A, located in City X. In order to show that we’re a great university, we want to prove that the students of University A perform better on a standardized test than the average student in City X. The board of the standardized test’s testing committee analyzed all the test scores and told us that students from City X average 75 points on the standardized test.

To see if our students actually perform better, we poll 100 students to share their test scores and find out that the average is 78 points with a standard deviation of 2.5 points. We also set a significance level (α) value of 0.05, which means the results are significant only if the P-value is below 0.05..

Since we are trying to prove that our students perform better on the test, our null hypothesis is that the average score of students at University A is not  above the city average.

We begin by calculating the Z-score for this test by subtracting the population mean (the City X average of 75) from our measured value (78) and dividing by the standard deviation (2.5) over the square root of the number of samples (100).

Z = (x – μ) / (σ / √n) = (78-75) / (2.5 / √100)

This gives us a Z-score of 12. Converting this Z-score gives us a very small P-value that’s less than 0.00001. That means that we can reject the null hypothesis. In other words, there’s statistically significant evidence that students of University A score more on average than other students in City X.

What can I use statistical significance for?

Now that you know how to calculate statistical significance, here are a few examples of places you can use statistical significance testing:

• Landing page conversions
• Notification / email response rates and conversion rates
• User reactions to product launches
• User reactions to pricing
• User reactions to a new design
• User reactions to newly launched features

Things to note

Statistical significance testing is a great tool to validate tests and analyses, but it doesn’t mean that your data is accurate or unbiased. Survey respondents can lie and give you incorrect information, and your surveys can be biased by a non-uniform representation of certain demographics.

Additionally, a poorly run statistical significance test can lead to inaccurate insights. This can happen when the significance level (α) chosen is incorrect.

Finally, P-values by definition allow for a small chance of a false positive. One way to counter this is reproducing the results. If you can repeat the study and achieve a low P-value, the likelihood that you observed a false positive is reduced.

Remember, statistical significance is a great tool to make business decisions with increased confidence, but it is not a mathematical silver bullet.